机器学习-概率生成模型
理论基础
概率生成模型,是概率统计和机器学习中的一类重要模型,指一系列用于随机生成可观测数据的模型。假设有两类数据,每一类都有若干个样本;概率生成模型认为每一类数据都服从某一种分布,如高斯分布;从两类训练数据中得到两个高斯分布的密度函数,具体的是获得均值和方差两个参数;测试样本输入到其中一个高斯分布函数,得到的概率值若大于0.5,则说明该样本属于该类,否则属于另一类。
生成模型可以和贝叶斯概率公式进行结合,用于分类问题。原始贝叶斯概率公式为:
\[ P(A|B)=\frac{P(B|A)P(A)}{P(B)} \tag{1} \]
对于一个\(2\times2\)的分类则有下图所述的贝叶斯分类
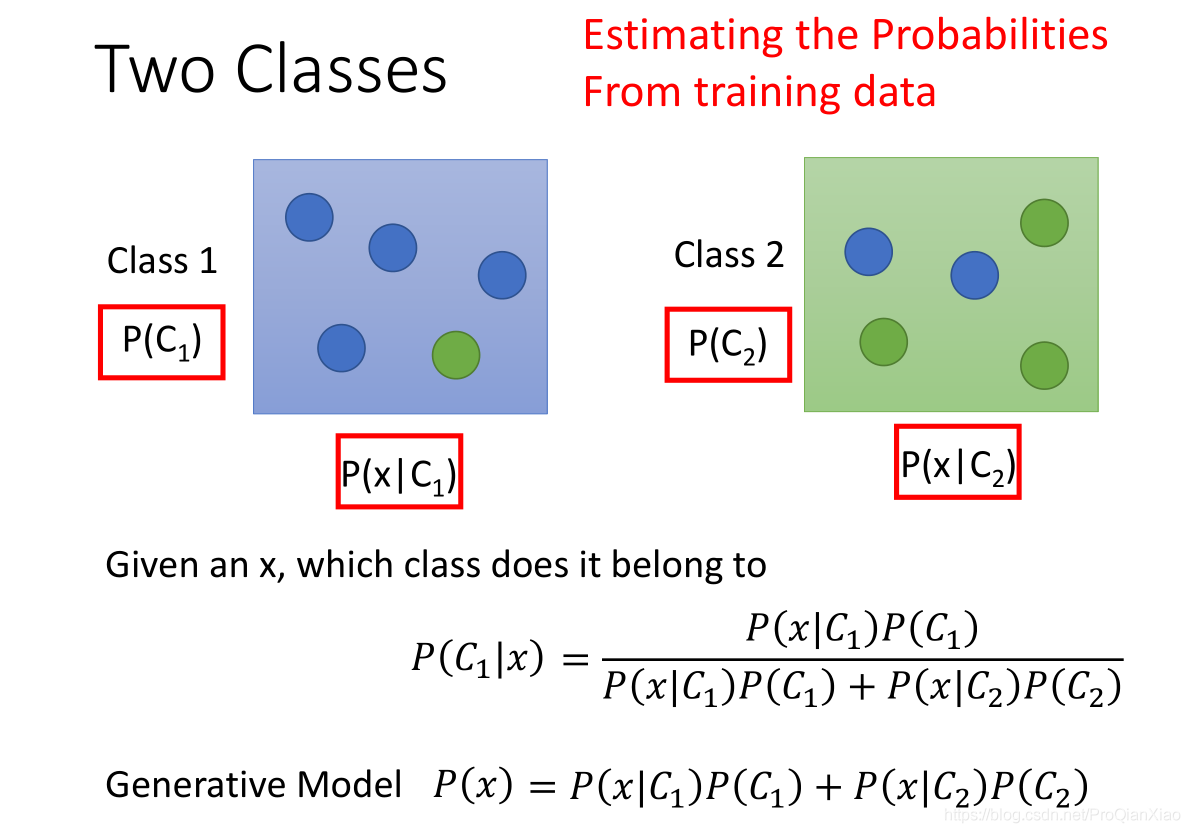
在上图中,训练数据中有两个类别;每个类别下有5个样本,我们想要知道新的测试样本\(x\)属于\(C1\)的可能性。根据贝叶斯概率公式可以得到上图片所示的概率公式。其中,\(P(C1)\)和\(P(C2)\)表示在训练数据中,随机采样得到\(C1\)或者C2的概率,即两个类别在训练数据中所占的比重。分母项\(P(x)\)表示生成数据x的概率,此处可以由生成模型计算得到;
\[ P(x) = P(x|C1)P(C1) + P(x|C2)P(C2) \]
因为有两个类别,每个类别下的数据具有不同的规律,服从不同的分布,都有可能生成数据\(x\),所以相加得到生成\(x\)的概率。\(P(C1)\)和\(P(C2)\)可以由训练数据中的统计结果计算得到。
接下来是计算\(P(x|C1)\)和\(P(x|C2)\),我们一般是采用最大似然估计来计算。
给定一个概率分布D,假定其概率密度函数(连续分布)或概率聚集函数(离散分布)为\(f_D\),以及一个分布参数\(θ\),我们可以从这个分布中抽出一个具有n个值的采样\(X_1,X_2,...,X_n\),通过利用\(f_D\),我们就能计算出其概率:
\[ P=(x_1,x_2,...,x_n)=f_D(x_1,x_2,...,x_n|\theta) \]
但是,我们可能不知道θ的值,尽管我们知道这些采样数据来自于分布D。那么我们如何才能估计出θ呢?一个自然的想法是从这个分布中抽出一个具有n个值的采样\(X_1,X_2,...,X_n\),然后用这些采样数据来估计θ。 要在数学上实现最大似然估计法,我们首先要定义可能性:
\[ lik(\theta)=f_D(x_1,x_2,...,x_n|\theta) \]
并且在\(θ\)的所有取值上,使这个函数最大化。这个使可能性最大的值即被称为θ的最大似然估计。
实例
在此进行一个宝可梦类别的分类工作:我们使用两个类别的宝可梦构成训练数据,分别是水系(Water)和正常系(Normal),数据构成如下:

根据贝叶斯概率公式,计算P(x|C1)和P(x|C2)。分析每个类别下的数据分布规律,计算新的测试数据x分别由每个类别的数据模型生成的概率。
每个宝可梦,有两个特征属性 Defence 和 SP Defence,假设数据的分布符合高斯分布。
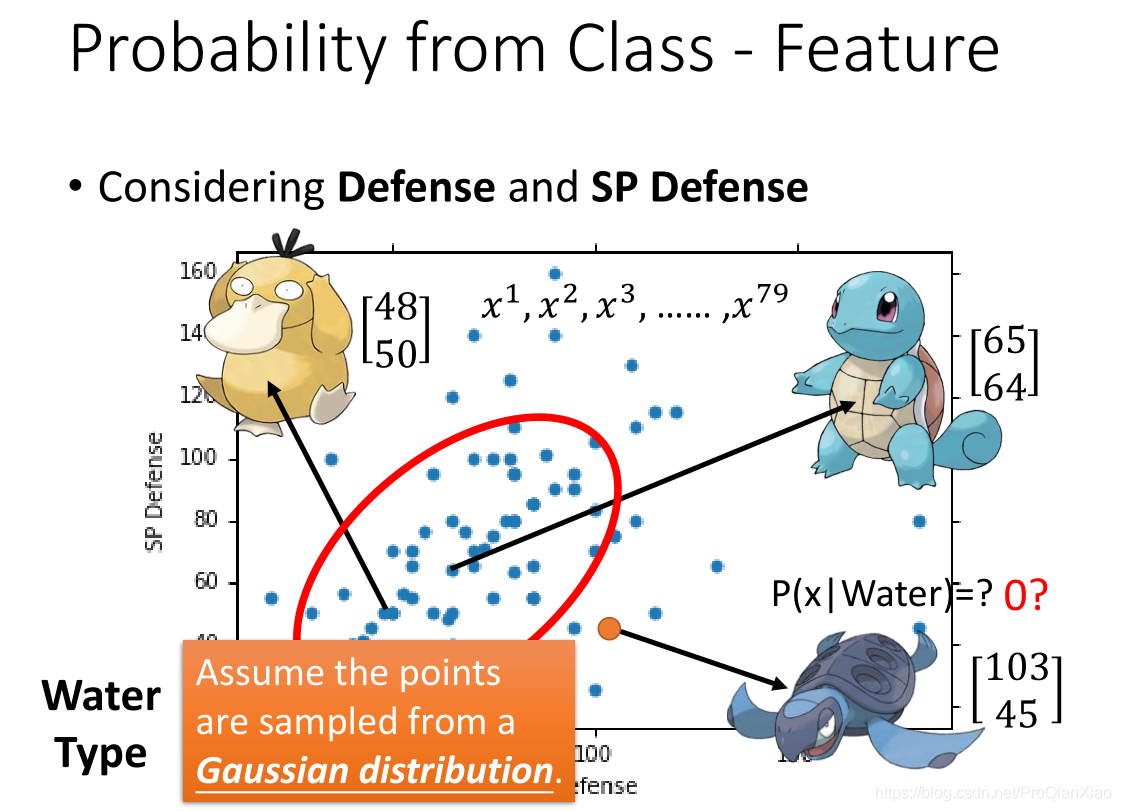
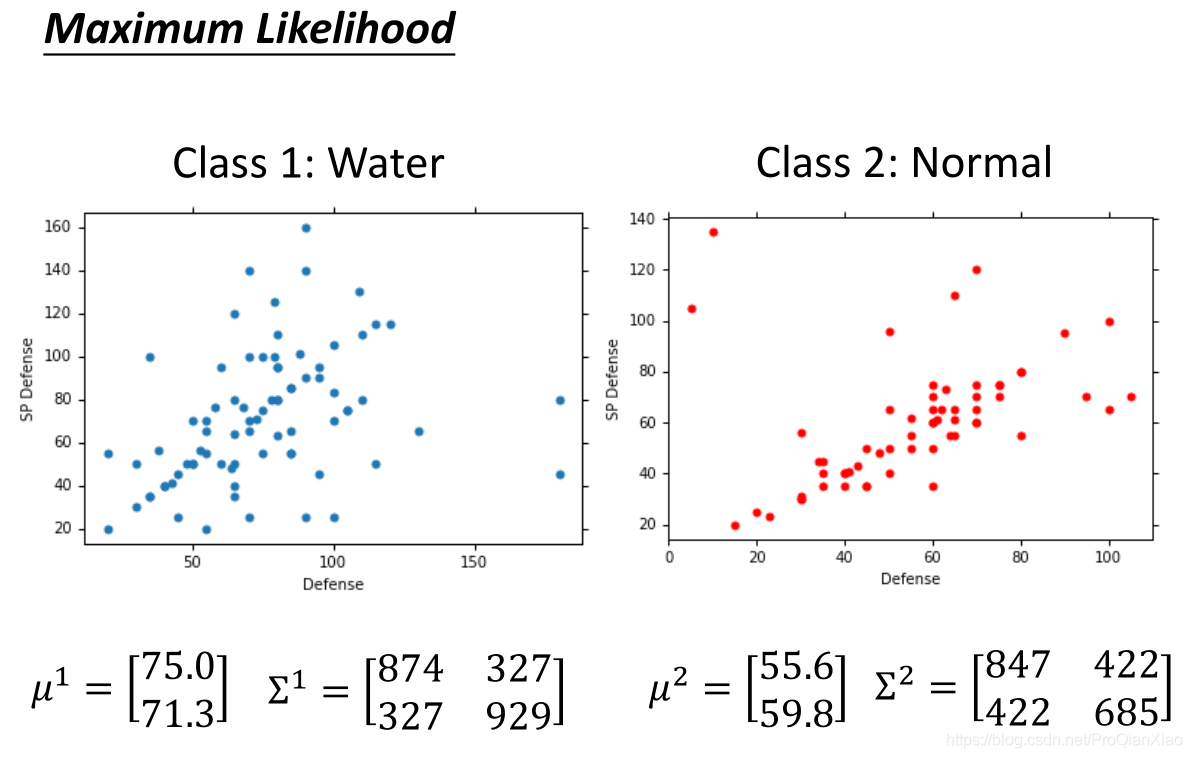
接着由极大似然估计法,计算得到高斯分布的参数,即均值和标准差。
- 均值表征的是各维变量的中心
- 协方差矩阵的对角线上的两个元素,决定了整个高斯曲面在某一维度上的“跨度”,方差越大,“跨度”越大
- 协方差矩阵的斜对角线上面的两个元素,表征的是各维变量之间的相关性,其数值大于零说明x与y呈正相关,其值越大,正相关程度越大,小于零则是负相关,否则则是不相关
接着,使用贝叶斯概率公式进行分类

测试数据上的准确率为47%,效果很差。使用更多特征之后,准确率为54%
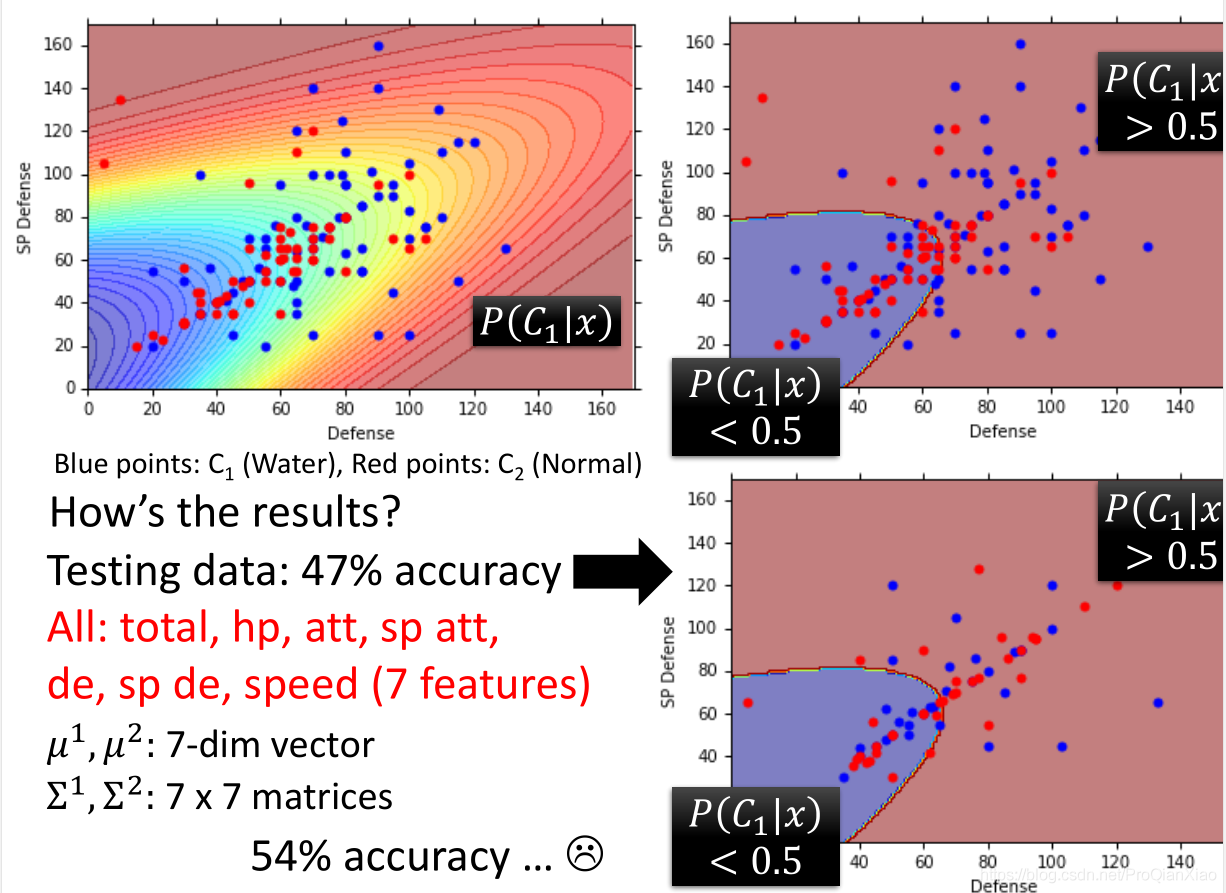
那么则需要对模型进行调整,也就是调整高斯分布的均值和标准差
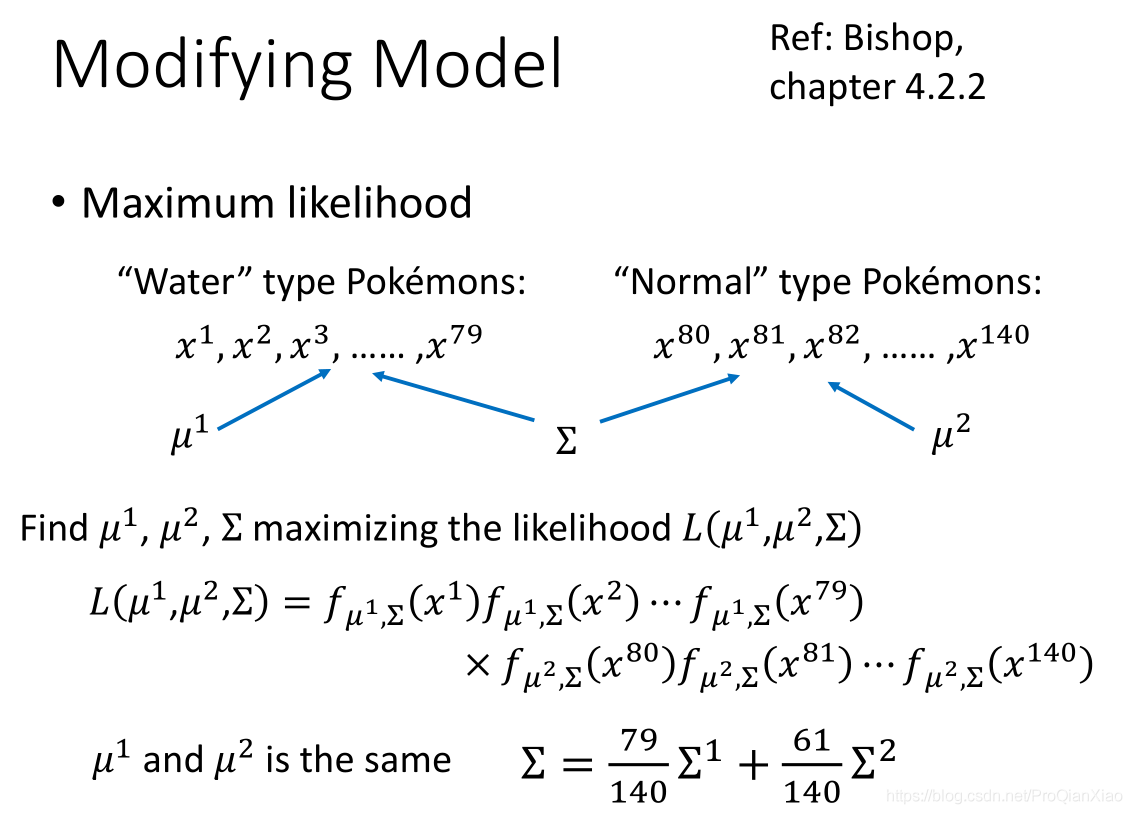
这里使水系宝可梦和普通系宝可梦使用一个标准差矩阵,计算方式为其二者加权平均,使其准确率得到了一定的提升。
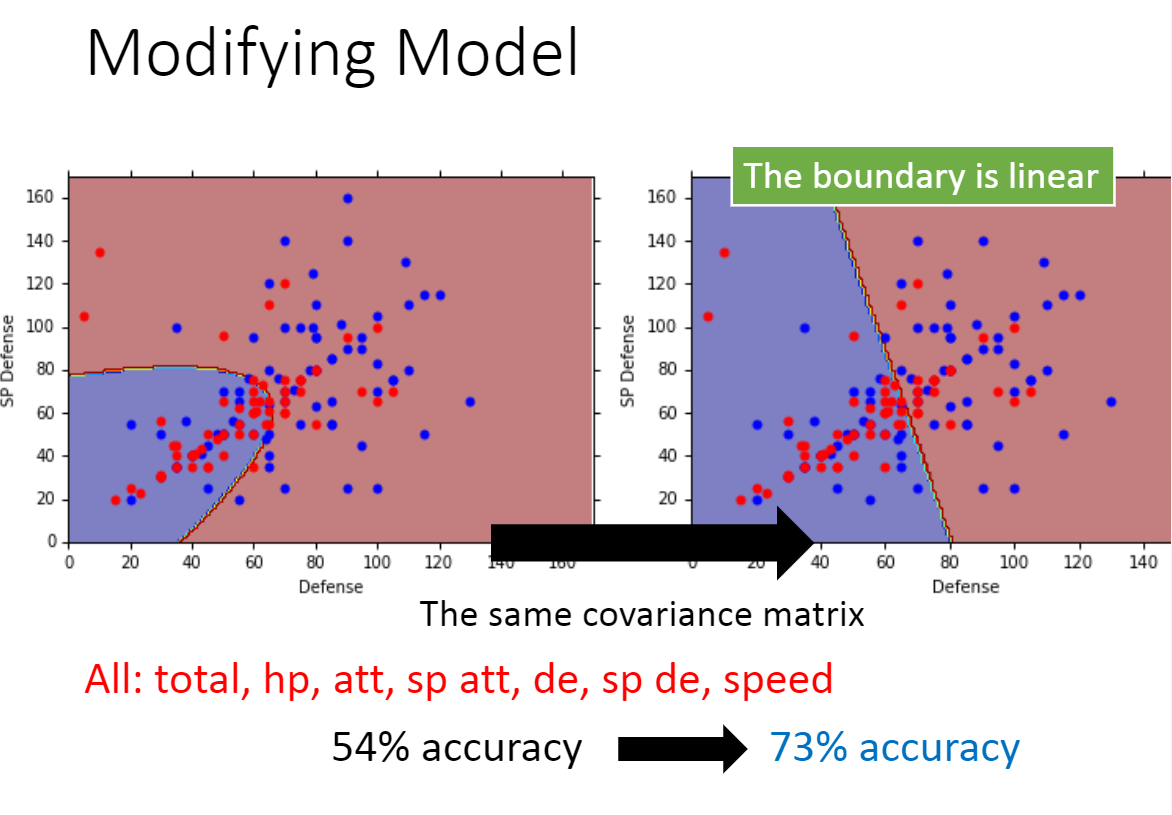
总结
概率生成模型进行分类问题的三个步骤如下:

后续
之前我们有贝叶斯的公式,那么能够将其进行简化呢?






经过最终的化简计算可以知道,概率生成模型的本质是寻找参数w和b。如果我们直接进行参数w和b的求解,是不是就可以简化前面那么复杂的计算过程呢?那么请看下一篇博客吧。